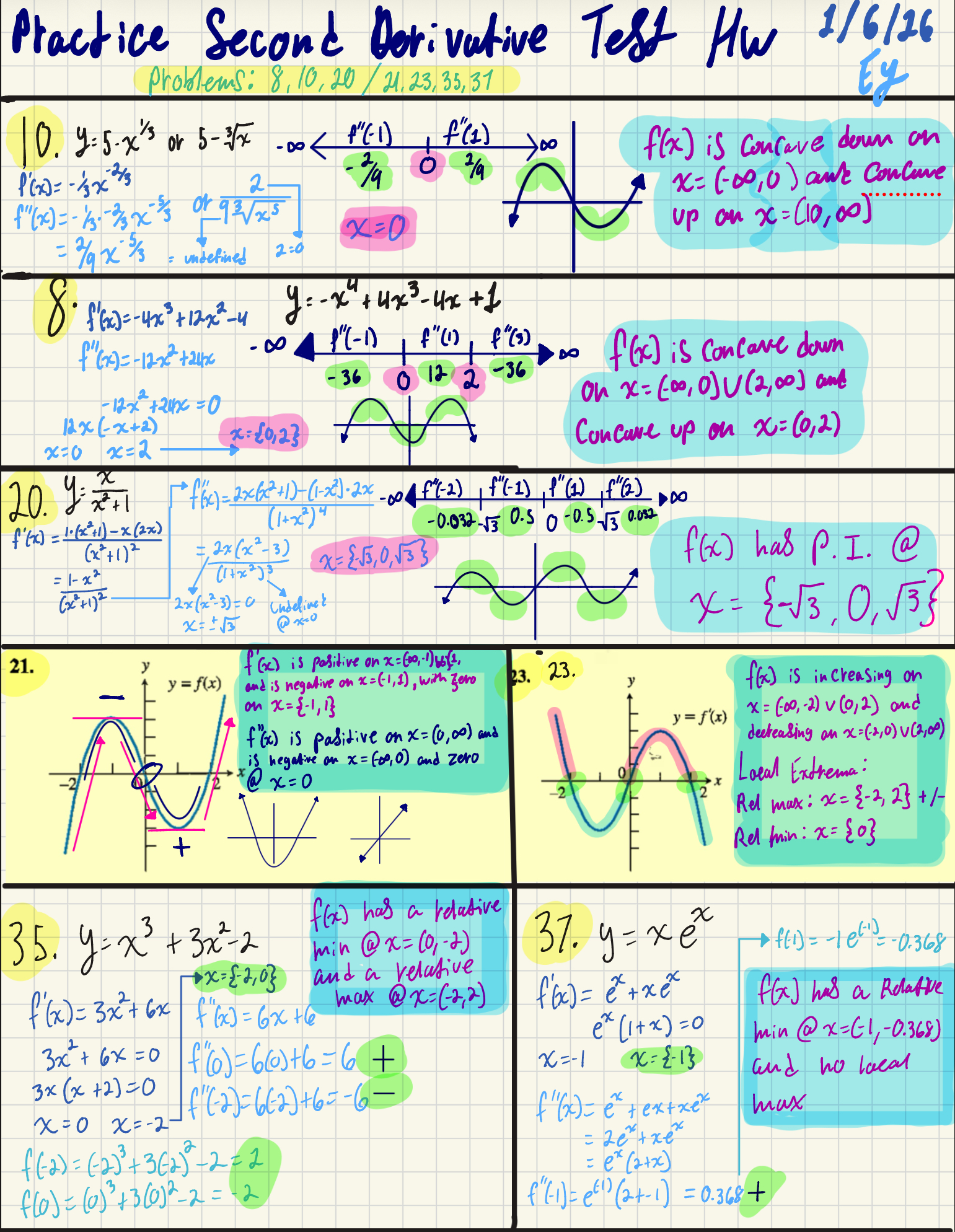
practice Second Derivative Test Hw 1/6/16 Ey
problems: 8,10,20 / 21,23,35,31
10. y=5-x's y: or 5-3/x -DO
f"(-1)
f"(1)
1
8
f(x) is Concave down on
P'(x)= 1/3X2/3
all
O
1/9
2
X= (-00,0) amt ConCuve
or
93Vx5
X=0
up on x=(10,00)
"
=2/9 x-5/3
: undefined
2:0
8. f(x)=-4x3 +12x2-4
Y=-x4 t 4x 4x +1
-00
p"(-1)
f"(1)
f"(3)
8
f(x) is Concave down
36
0
12
2
36
-12-2+24x=0
on x=(xx,0)V(2,00) and
12x (-x+2)
x={0,2}
Concave up on x=(0,2)
x=0 x=2
20. Y.X x
f"(-2)
f"(-1)
8
, (1)
f"(2)
8
(1+x²)⁴
-0.032-53 0.5 0-0.5-13 0.032
(x²+1)²
= 2x(x²-3)
11
x={-5,0,53}
f(x) has P.I. @
=1-x2 =
(1+x2)
(x*+1)2
2x(x23)=c
Chdelivek
X= {-53, O,
X=t5
@x10
21.
y
f(x) is positive on
y=f(x) f(x)
and is negative on x=(1,1), with Zero
23. 23.
1
y
f(x) is increasing on
-
on x={-1,1}
and
y=f'(x) =
f"(x) is pasitive on x=(0,00) and
decreasing an x=(2,0)V(2,00)
is hegative an x=(-00,0) and zero
-2
x @ x=0
0
Local Extrema:
2
AN
x
-2
2
Rel mux: x=8-2,2}+/-
+
Rel min: x= {o}
f(x) has a relative
35. Y=x3 3 + 3x2-2
min @ x=(0,-2)
37. y = x e
f(1) = =-0,368
x={-2,0}
and a relative
f'(x)= f'(x)=3x²+6x = 3x2+ 6x
max @ x=(-2,2)
f'(x)= ex + xêx
f(x) has a Relative
f"(x)=6x+6
ex(1+x)=0
min @x=(-1,-0.368)
3x2+ 6x =
f"(0)=66)+6 = +
X=-1
x={-1}
and no Iceal
3x(x+2)=0
f"(-2)=62)+6=-6-
f"(x)= e textxex
max
X=0 = X=2
=2extxex
=
: ex(2+x)
f"(-1)= (2+1) =0.368+