Study Guide
Chapter 8 Work, Power & Energy
-
University:
California State University, Chico -
Course:
PHYS 202A | General Physics I Academic year:
2021
-
Views:
391
Pages:
31
Author:
Prince Sampson
= =– =– T t t v u gt 2 − usin (ii) Instantaneous power
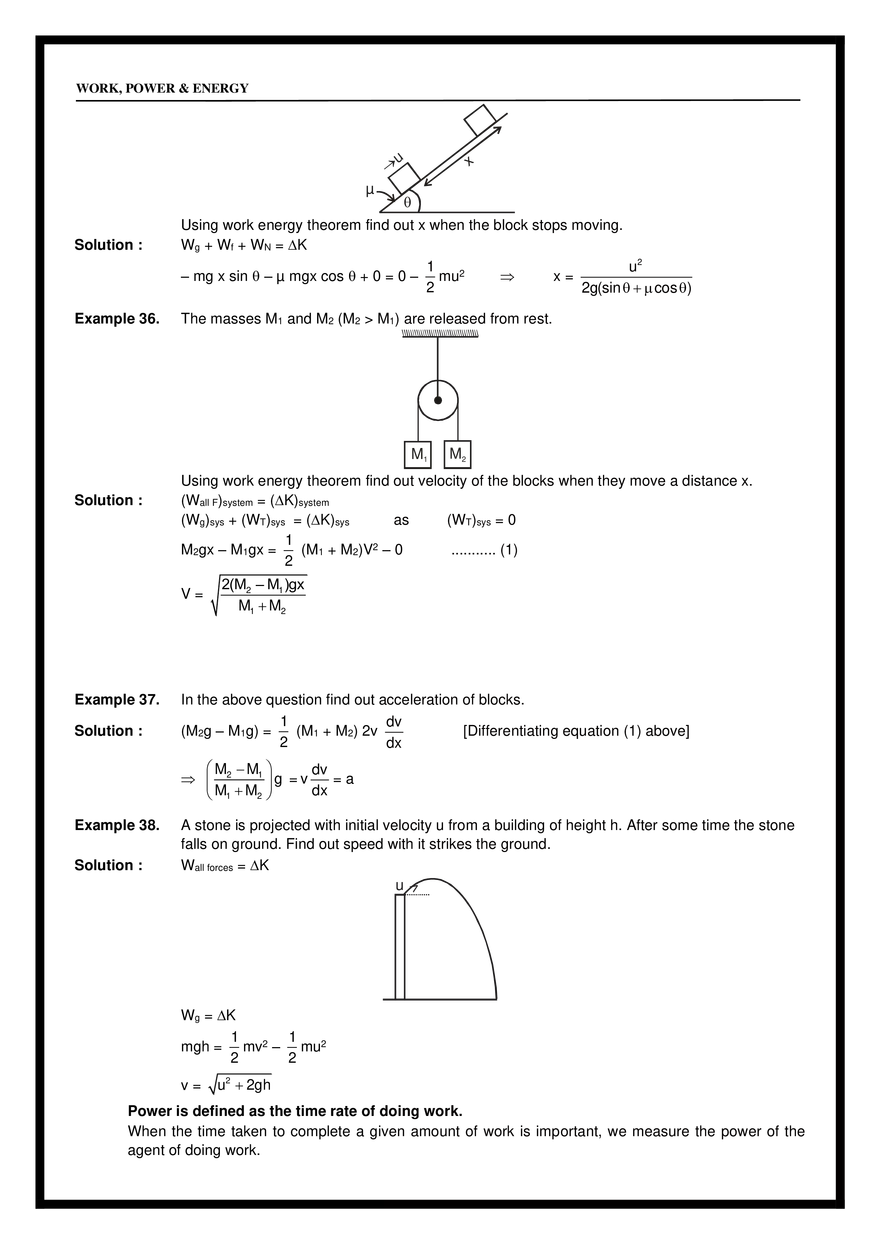
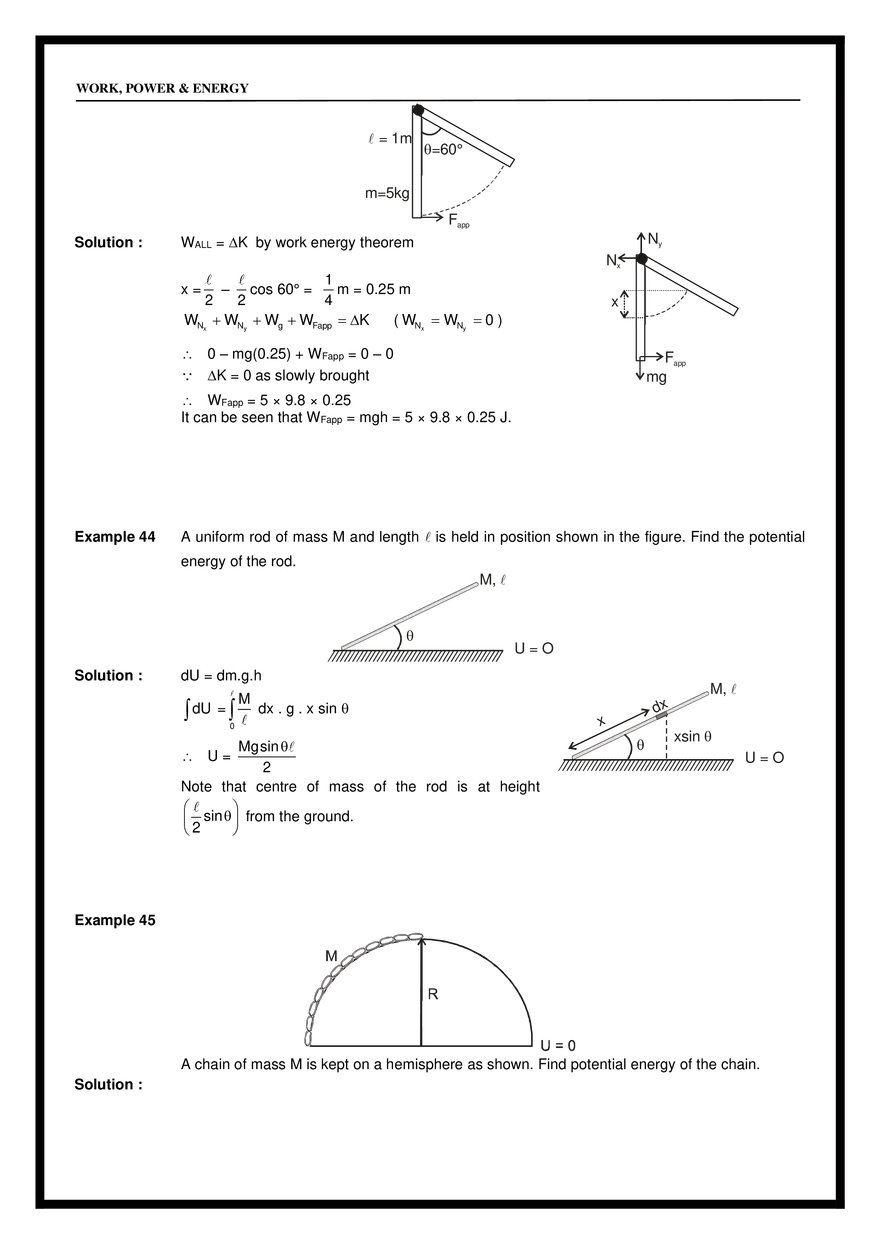
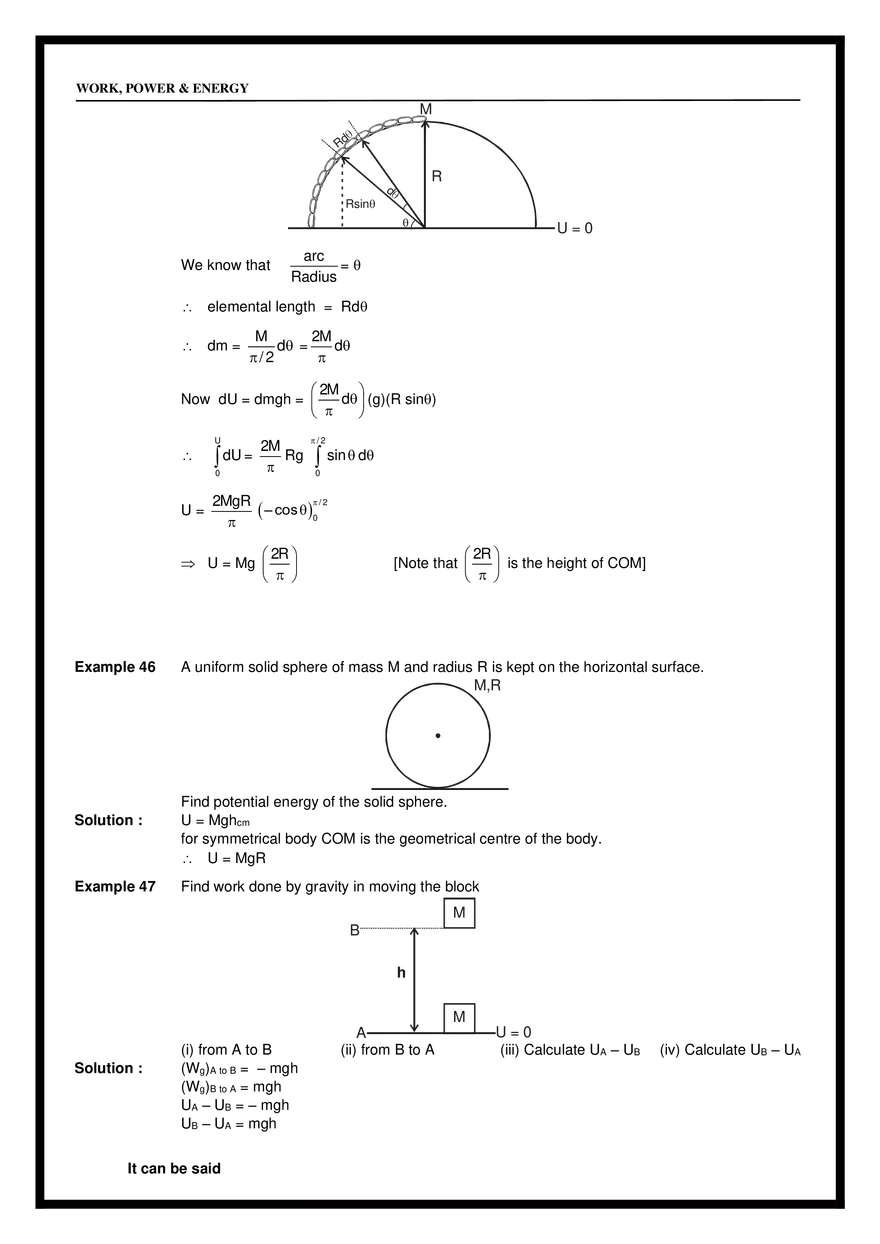
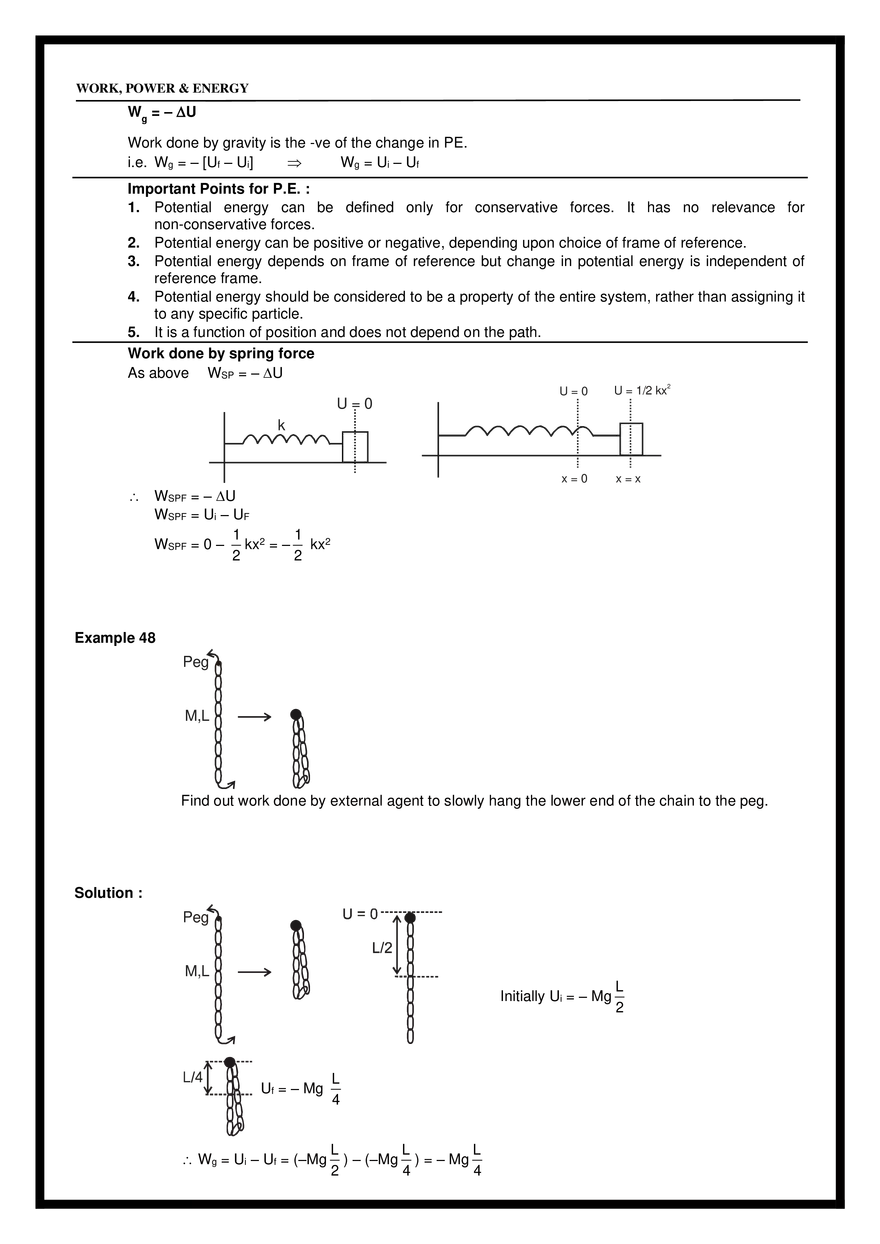
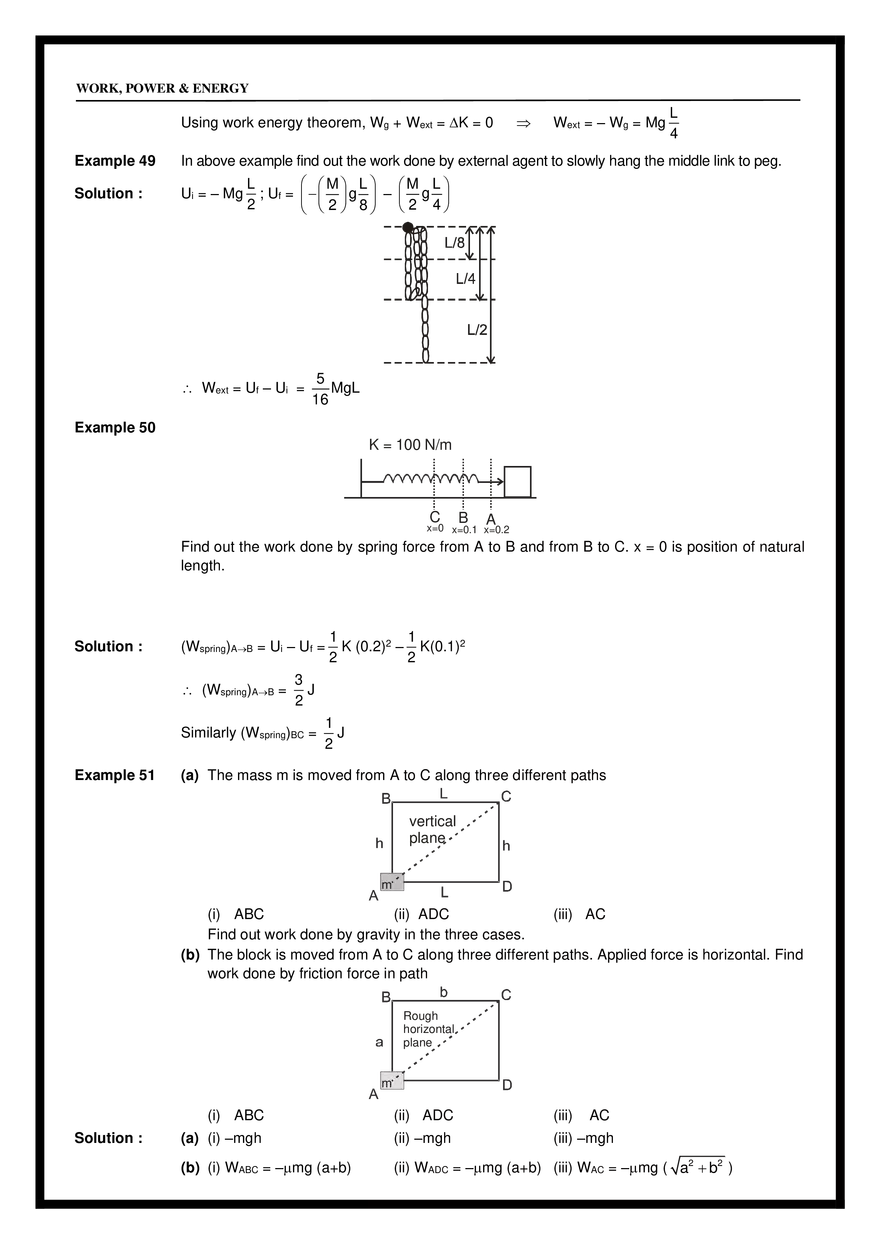
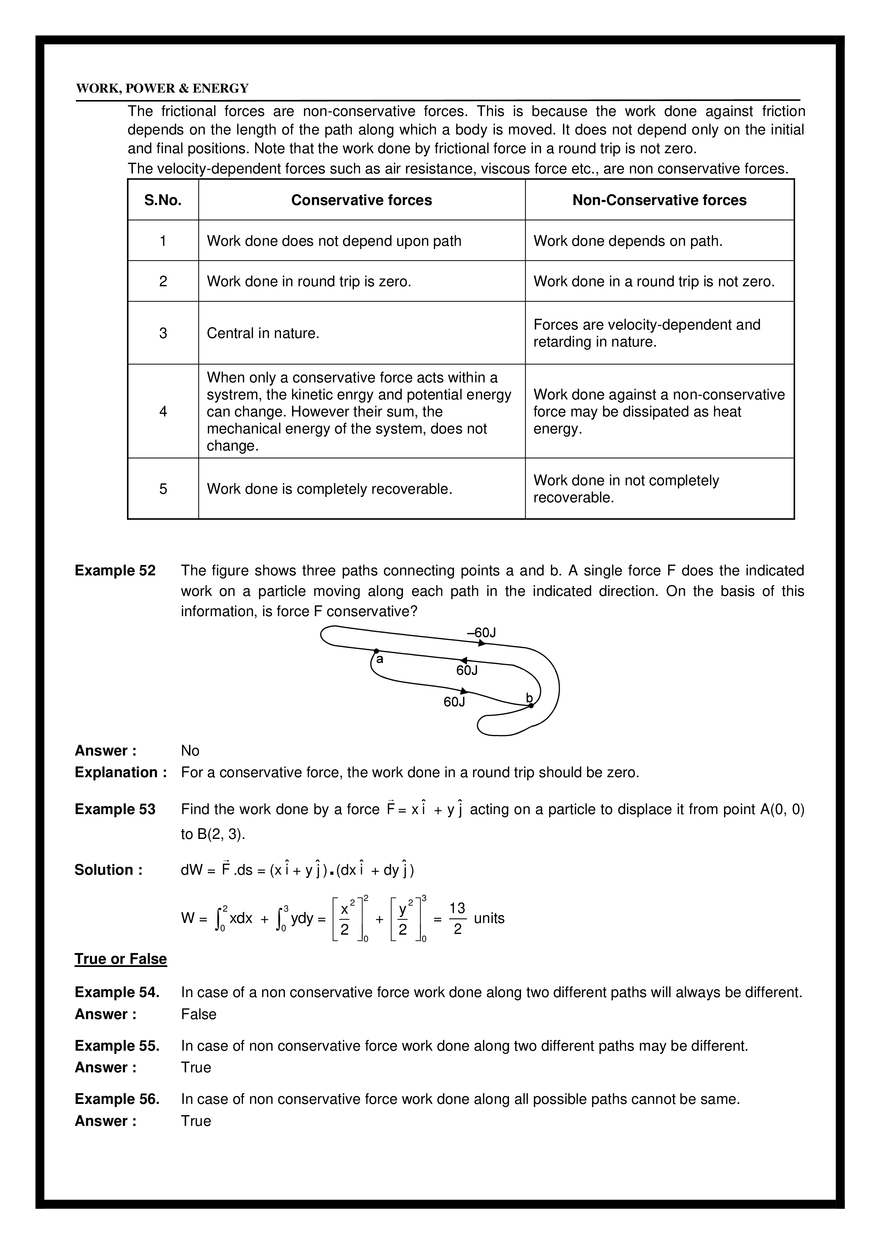
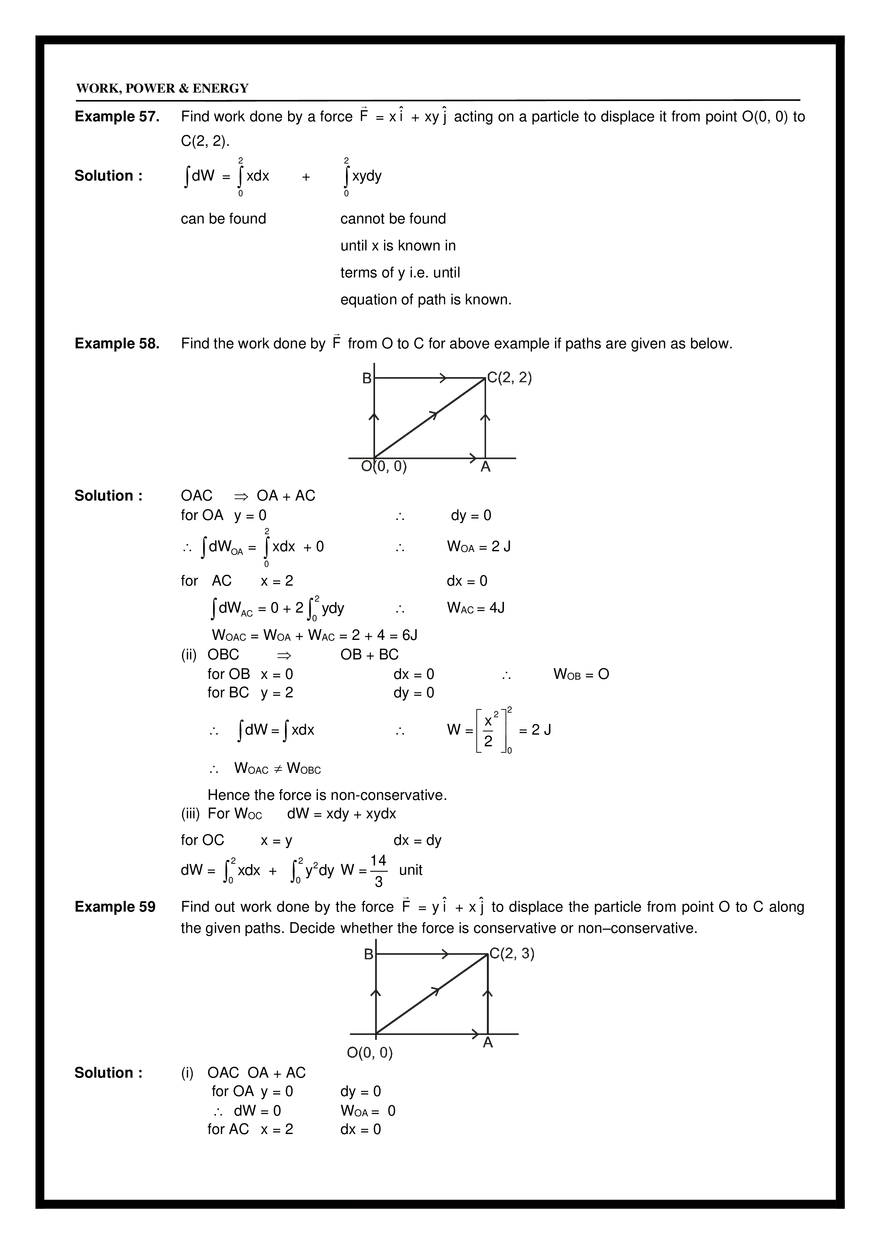
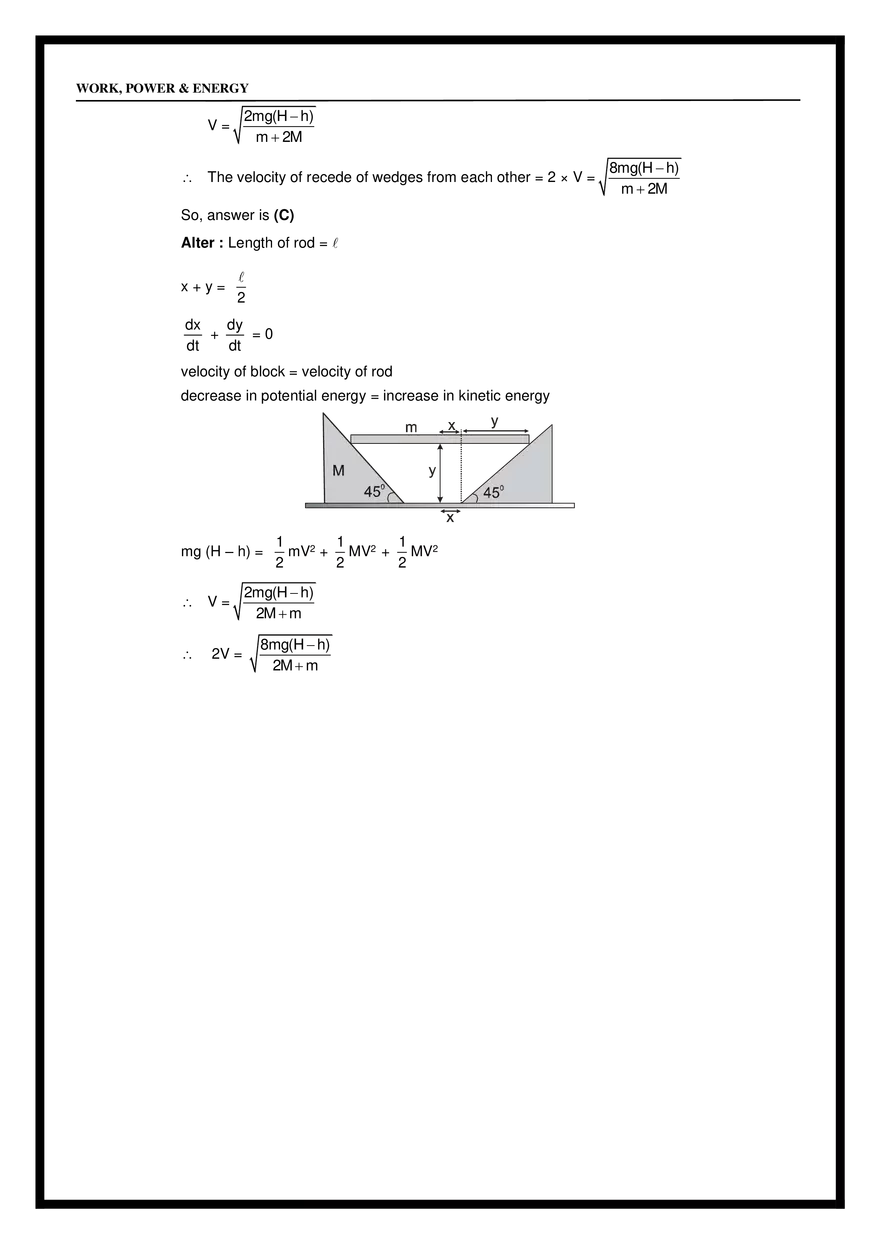
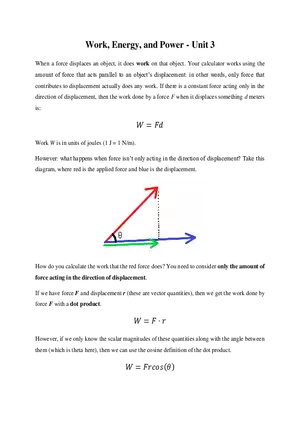
= mg P = F v = (–mg ĵ ) [ucos î + (usin – gt)) ĵ ] = –mg(usin – gt) gt 2usin = u sin (iii) t= , 2 g (iv) When F & V are ⊥ i.e. at t = i.e. time of flight. usin which is at the highest point. g (v) From base to highest point. (vi) From highest point to base. POTENTIAL ENERGY Energy : It is the internal capacity to do work. Kinetic Energy : It is internal capacity to do work by virtue of relative motion. Potential Energy : It is the internal capacity to do work by virtue of relative position. h WORK, POWER & ENERGY Example : Gravitational Potential Energy , Spring PE etc. Potential Energy Definition: Potential energy is the internal capacity of doing work of a system by virtue of its configuration. In case of conservative force (field) potential energy is equal to negative of work done by the conservative force in shifting the body from some reference position to given position. Therefore, in case of conservative force U2 U1 r2 dU = − F dr r1 i.e. U2 − U1 = − r2 r1 F dr = −W Whenever and wherever possible, we take the reference point at and assume potential energy to be zero there, i.e., If we take r1 = and U1 = 0 then r U = − F dr = − W (a) Gravitation Potential Energy : U = mgh for a particle at a height h above reference level. Example 42 Calculate potential energy of a uniform vertical rod of mass M and length . M Solution : dU = (dm) gx M dx x M U dU = 0 U= 0 dx gx Mg 2 (b) Spring potential energy : 1 U = Kx 2 2 Where x is change in length from its natural length. Note : Gravitational potential energy can be +ve , –ve or zero but spring potential energy will always be +ve. Example 43 In the given figure, a uniform rod of mass m and length l is hinged at one end. Find the work done by applied force in slowly bringing the rod to the inclined position. WORK, POWER & ENERGY ⚫ = 1m =60° m=5kg Fapp Solution : WALL = K by work energy theorem Ny Nx 1 – cos 60° = m = 0.25 m 2 2 4 WNx + WNy + Wg + WFapp = K ( WNx = WNy = 0 ) x= ⚫ x 0 – mg(0.25) + WFapp = 0 – 0 K = 0 as slowly brought Fapp mg WFapp = 5 × 9.8 × 0.25 It can be seen that WFapp = mgh = 5 × 9.8 × 0.25 J. Example 44 A uniform rod of mass M and length is held in position shown in the figure. Find the potential energy of the rod. M, Solution : U=O dU = dm.g.h dU = M dx . g . x sin 0 Mgsin 2 Note that centre of mass of the rod is at height 2 sin from the ground. U= M, dx x xsin U=O Example 45 A chain of mass M is kept on a hemisphere as shown. Find potential energy of the chain. Solution : WORK, POWER & ENERGY M Rd R d Rsin We know that U=0 arc = Radius elemental length = Rd dm = M 2M d = d /2 2M d (g)(R sin) Now dU = dmgh = U dU = 0 U= 2M Rg /2 sin d 0 /2 2MgR ( – cos )0 2R [Note that is the height of COM] 2R U = Mg Example 46 Solution : Example 47 A uniform solid sphere of mass M and radius R is kept on the horizontal surface. M,R Find potential energy of the solid sphere. U = Mghcm for symmetrical body COM is the geometrical centre of the body. U = MgR Find work done by gravity in moving the block M B h M Solution : (i) from A to B (Wg)A to B = – mgh (Wg)B to A = mgh UA – UB = – mgh UB – UA = mgh It can be said A (ii) from B to A U=0 (iii) Calculate UA – UB (iv) Calculate UB – UA WORK, POWER & ENERGY Wg = – U Work done by gravity is the -ve of the change in PE. i.e. Wg = – [Uf – Ui] Wg = Ui – Uf Important Points for P.E. : 1. Potential energy can be defined only for conservative forces. It has no relevance for non-conservative forces. 2. Potential energy can be positive or negative, depending upon choice of frame of reference. 3. Potential energy depends on frame of reference but change in potential energy is independent of reference frame. 4. Potential energy should be considered to be a property of the entire system, rather than assigning it to any specific particle. 5. It is a function of position and does not depend on the path. Work done by spring force As above WSP = – U U=0 U = 1/2 kx x=0 x=x 2 U=0 k WSPF = – U WSPF = Ui – UF 1 1 WSPF = 0 – kx2 = – kx2 2 2 Example 48 Peg M,L ⚫ Find out work done by external agent to slowly hang the lower end of the chain to the peg. Solution : Peg ⚫ M,L Initially Ui = – Mg Uf = – Mg Wg = Ui – Uf = (–Mg L 4 L L L ) – (–Mg ) = – Mg 2 4 4 L 2 WORK, POWER & ENERGY Using work energy theorem, Wg + Wext = K = 0 Wext = – Wg = Mg L 4 Example 49 In above example find out the work done by external agent to slowly hang the middle link to peg. Solution : Ui = – Mg L ; Uf = 2 M L M L − g – g 2 8 2 4 Wext = Uf – Ui = 5 MgL 16 Example 50 K = 100 N/m C B A x=0 x=0.1 x=0.2 Find out the work done by spring force from A to B and from B to C. x = 0 is position of natural length. Solution : (Wspring)A→B = Ui – Uf = (Wspring)A→B = 3 J 2 Similarly (Wspring)BC = Example 51 1 1 K (0.2)2 – K(0.1)2 2 2 1 J 2 (a) The mass m is moved from A to C along three different paths vertical plane (i) ABC (ii) ADC (iii) AC Find out work done by gravity in the three cases. (b) The block is moved from A to C along three different paths. Applied force is horizontal. Find work done by friction force in path Rough horizontal plane Solution : (i) ABC (ii) ADC (iii) AC (a) (i) –mgh (ii) –mgh (iii) –mgh (b) (i) WABC = –mg (a+b) (ii) WADC = –mg (a+b) (iii) WAC = –mg ( a2 + b2 ) WORK, POWER & ENERGY CONSERVATIVE FORCES A force is said to be conservative if work done by or against the force in moving a body depends only on the initial and final positions of the body and not on the nature of path followed between the initial and final positions. Consider a body of mass m being raised to a height h vertically upwards as show in above figure. The work done is mgh. Suppose we take the body along the path as in (b). The work done during horizontal motion is zero. Adding up the works done in the two vertical parts of the paths, we get the result mgh once again. Any arbitrary path like the one shown in (c) can be broken into elementary horizontal and vertical portions. Work done along the horizontal parts is zero. The work done along the vertical parts add up to mgh. Thus we conclude that the work done in raising a body against gravity is independent of the path taken. It only depends upon the initial and final positions of the body. We conclude from this discussion that the force of gravity is a conservative force. Examples of Conservative forces. (i) Gravitational force, not only due to the Earth but in its general form as given by the universal law of gravitation, is a conservative force. (ii) Elastic force in a stretched or compressed spring is a conservative force. (iii) Electrostatic force between two electric charges is a conservative force. (iv) Magnetic force between two magnetic poles is a conservative forces. In fact, all fundamental forces of nature are conservative in nature. Forces acting along the line joining the centres of two bodies are called central forces. Gravitational force and Electrostatic forces are two important examples of central forces. Central forces are conservative forces. PROPERTIES OF CONSERVATIVE FORCES (i) Work done by or against a conservative force depends only on the initial and final positions of the body. (ii) Work done by or against a conservative force does no depend upon the nature of the path between initial and final positions of the body. If the work done a by a force in moving a body from an initial location to a final location is independent of the path taken between the two points, then the force is conservative. (iii) Work done by or against a conservative force in a round trip is zero. If a body moves under the action of a force that does no total work during any round trip, then the force is conservative; otherwise it is non-conservative. The concept of potential energy exists only in the case of conservative forces. (iv) The work done by a conservative force is completely recoverable. Complete recoverability is an important aspect of the work of a conservative force. NON-CONSERVATIVE FORCES A force is said to be non-conservative if work done by or against the force in moving a body depends upon the path between the initial and final positions. WORK, POWER & ENERGY The frictional forces are non-conservative forces. This is because the work done against friction depends on the length of the path along which a body is moved. It does not depend only on the initial and final positions. Note that the work done by frictional force in a round trip is not zero. The velocity-dependent forces such as air resistance, viscous force etc., are non conservative forces. S.No. Conservative forces Non-Conservative forces 1 Work done does not depend upon path Work done depends on path. 2 Work done in round trip is zero. Work done in a round trip is not zero. 3 Central in nature. Forces are velocity-dependent and retarding in nature. 4 When only a conservative force acts within a systrem, the kinetic enrgy and potential energy can change. However their sum, the mechanical energy of the system, does not change. Work done against a non-conservative force may be dissipated as heat energy. 5 Work done is completely recoverable. Work done in not completely recoverable. Example 52 The figure shows three paths connecting points a and b. A single force F does the indicated work on a particle moving along each path in the indicated direction. On the basis of this information, is force F conservative? Answer : No Explanation : For a conservative force, the work done in a round trip should be zero. Example 53 Find the work done by a force F = x î + y ĵ acting on a particle to displace it from point A(0, 0) to B(2, 3). Solution : . dW = F .ds = (x î + y ĵ ) (dx î + dy ĵ ) 2 3 x2 y2 13 W = xdx + ydy = + = units 0 0 2 2 0 2 0 2 3 True or False Example 54. Answer : In case of a non conservative force work done along two different paths will always be different. False Example 55. Answer : In case of non conservative force work done along two different paths may be different. True Example 56. Answer : In case of non conservative force work done along all possible paths cannot be same. True WORK, POWER & ENERGY Example 57. Find work done by a force F = x î + xy ĵ acting on a particle to displace it from point O(0, 0) to C(2, 2). Solution : 2 2 xdx dW = xydy + 0 0 can be found cannot be found until x is known in terms of y i.e. until equation of path is known. Example 58. Find the work done by F from O to C for above example if paths are given as below. Solution : OAC OA + AC for OA y = 0 dy = 0 WOA = 2 J 2 dW OA = xdx +0 0 for AC x=2 dW AC dx = 0 2 = 0 + 2 ydy 0 WAC = 4J WOAC = WOA + WAC = 2 + 4 = 6J (ii) OBC OB + BC for OB x = 0 dx = 0 for BC y = 2 dy = 0 WOB = O 2 dW = xdx x2 W = = 2 J 2 0 WOAC WOBC Hence the force is non-conservative. (iii) For WOC dW = xdy + xydx for OC dW = x=y 2 0 xdx + dx = dy 2 0 y 2 dy W = 14 unit 3 Example 59 Find out work done by the force F = y î + x ĵ to displace the particle from point O to C along the given paths. Decide whether the force is conservative or non–conservative. Solution : (i) OAC OA + AC for OA y = 0 dW = 0 for AC x = 2 dy = 0 WOA = 0 dx = 0 WORK, POWER & ENERGY 3 dW = 2 dy W=6J WOAC = 6 units 0 (ii) OBC for OB x=0 for BC y=3 dW = 2 0 OB + BC dx = 0 dy = 0 3dx dW = 0 W = 6 units WOBC = 6 units (iii) OC 3 x 2 for OC y = dW = dy = 3 dx 2 2 2 2 3 3 0 2 xdx + 0 2 xdx dW = 3 x dx WOC = 6 units 0 Above force seems conservative but cannot be confirmed yet unless we can integrate it without the knowledge of path. Again we had dw = xdy + ydx & xdy + ydx can be written as dxy dW = dxy W= 2,3 0,0 2,3 dxy = xy 0,0 = 6J Hence knowledge of path was not required to integrate the above so F is conservative. POTENTIAL ENERGY AND CONSERVATIVE FORCE : FS = – U/ s, i.e., the projection of the field force, the vector F, at a given point in the direction of the displacement dr equals the derivative of the potential energy U with respect to a given direction, taken with the opposite sign. The designation of a partial derivative / s emphasizes the fact of deriving with respect to a definite direction. So, having reversed the sign of the partial derivatives of the function U with respect to x, y, z, we obtain the projection Fx, Fy and Fz of the vector F on the unit vectors i, j and k. Hence, one can readily find the vector itself : F = Fxi + Fyj + Fzk, or When conservative force does positive work then PE decreases dU = – dw dU = – F.ds dU = – (Fx î + Fy ĵ + Fz k̂ ) . (dx î + dy ĵ + dz k̂ ) dU = – Fxdx – Fydy – Fzdz if y & z are constants then dy = 0 dz = 0 dU = –Fxdx Fx = – Fx = dU if y & z are constant dx −U x Similarly Fy = −u ; y Fz = −u z U U U i+ j+ k . F=– y z x The quantity in parentheses is referred to as the scalar gradient of the function U and is denoted by grad U or U. We shall use the second, more convenient, designation where (“nabla”) signifies the symbolic vector or operator = i + j +k x y z Potential Energy curve : ⚫ A graph plotted between the PE a particle and its displacement from the centre of force field is called PE curve. WORK, POWER & ENERGY ⚫ Using graph, we can predict the rate of motion of a particle at various positions. dU dx Case-I : On increasing x, if U increases, force is in (–) ve x direction i.e. attraction force. Case-II : On increasing x, if U decreases, force is in (+) ve x-direction i.e. repulsion force. ⚫ Force on the particle is F(x) = – Example 60. The potential energy of spring is given by U = 1 2 kx , where x is extension spring. Find the force 2 associated with this potential energy. −u = – kx x Solution : Fx = Fy = 0 Fz = 0. Example 61. The potential energy of a particle in a space is given by U = x 2 + y2. Find the force associated with this potential energy. Solution : Fx = −u = – [2x + 0] = – 2x x Fy = −u = – (2y + 0) = – 2y ; F = – 2x î – 2y ĵ y Example 62. Find out the potential energy of given force F = – 2x î – 2y ĵ . Solution : dU = –dW dU = −(−2xiˆ − 2yj)ˆ • (dxiˆ + dyj)ˆ dU = 2xdx + 2ydy U = x2 + y2 + C Example 63 Find out the potential energy of the force F = y î + x ĵ . Solution : dU = – dW dU = – (y î + x ĵ ) . (dx î + dy ĵ ) dU = −ydx + −xdy dU = − dxy U = –xy + c Example 64 Find out the force for which potential energy U = – xy. Solution : U ˆ U ˆ F = – i+ j y x F = y î + x ĵ Hence verifying the previous example. EQUILIBRIUM OF A PARTICLE Different positions of a particle : ( − xy) ˆ ( − xy) ˆ F = – i+ j y x WORK, POWER & ENERGY Position of equilibrium : If net force acting on a body is zero, it is said to be in equilibrium. For dU equilibrium = 0. Points P, Q & R are the states of equilibrium positions. dx Types of equilibrium : ⚫ Stable equilibrium : When a particle is displaced slightly from a position and a force acting on it brings it back to the initial position, it is said to be in stable equilibrium position. d2U dU Necessary conditions : – = 0, and = +ve dx 2 dx ⚫ Unstable Equilibrium : When a particle is displaced slightly from a position and force acting on it tries to displace the particle further away from the equilibrium position, it is said to be in unstable equilibrium. Condition : – ⚫ d2U dU = 0 potential energy is maximum i.e. = = – ve dx 2 dx Neutral equilibrium : In the neutral equilibrium potential energy is constant. When a particle is displaced from its position it does not experience any force acting on it and continues to be in equilibrium in the displaced position. This is said to be neutral equilibrium. A particle is in equilibrium if the acceleration of the particle is zero. As acceleration is frame dependent quantity therefore equilibrium depends on motion of observer also. Example 65 The potential energy between two atoms in a molecule is given by, U (x) = a b – 6 , where a 12 x x and b are positive constants and x is the distance between the atoms. The system is in stable equilibrium when (A) x = 0 Answer: (C) Solution : Given that, U(x) = We, know or 1/ 6 2a (C) x = b a (B) x = 2b F=– −6b 12a = 13 x7 x 11a (D) x = 5b b a – 6 x12 x du = (–12) a x–13 – (–6b) x–7 = 0 dx 1/ 6 or x6 = 12a/6b = 2a/b or 2a x= b 1/ 6 d2U 2a = +ve at x = 2 dx b u=0 Example 66. (A) (B) (E) (F) (C) E Earth (D) Moon of the cases above which is not a case of equilibrium. Solution : (F) as moon is always accelerated. It has centripetal acceleration or it is changing its velocity all the time. WORK, POWER & ENERGY Example 67. E G Solution : Find out positions of equilibrium and determine whether they are stable, unstable or neutral. Equilibrium is at B, D, F as force is zero here. For checking type of equilibrium displace slightly. We have B as stable equilibrium D as unstable equilibrium and F as neutral equilibrium Example 68. U E G Solution : Identify the points of equilibrium and discuss their nature. −U C, E, F are points of equilibrium because F = x When slope of U - x curve is zero then F is zero. Check stability through slopes at near by points. If we move right then slope should be positive for stable equilibrium and vice versa. In short it is like a hill and plateau. MECHANICAL ENERGY : Definition: Mechanical energy ‘E’ of an object or a system is defined as the sum of kinetic energy ‘K’ and potential energy ‘U’, i.e., E=K+U Important Points for M.E.: 1. It is a scalar quantity having dimensions [ML2T-2] and SI units joule. 2. It depends on frame of reference. 3. A body can have mechanical energy without having either kinetic energy or potential energy. However, if both kinetic and potential energies are zero, mechanical energy will be zero. The converse may or may not be true, i.e., if E = 0 either both PE and KE are zero or PE may be negative and KE may be positive such that KE + PE = 0. 4. As mechanical energy E = K + U, i.e., E - U = K. Now as K is always positive, E - U 0, i.e., for existence of a particle in the field, E U. 5. As mechanical energy E = K + U and K is always positive, so, if ‘U’ is positive ‘E’ will be positive. However, if potential energy U is negative, ‘E’ will be positive if K > |U| and E will be negative if K < |U| i.e., mechanical energy of a body or system can be negative, and negative mechanical energy means that potential energy is negative and in magnitude it is more than kinetic energy. Such a state is called bound state, e.g., electron in an atom or a satellite moving around a planet are in bound state. Example 69 As shown in figure there is a spring block system. Block of mass 500 g is pressed against a horizontal spring fixed at one end to compress the spring through 5.0 cm. The spring constant WORK, POWER & ENERGY is 500 N/m. When released, the block moves horizontally till it leaves the spring. Calculate the distance where it will hit the ground 4 m below the spring? Solution : When block released, the block moves horizontally with speed V till it leaves the spring. 1 2 1 kx = mv2 2 2 By energy conservation V2 = kx 2 m V= Time of flight t = kx 2 m 2H g So, horizontal distance travelled from the free end of the spring is V × t = kx 2 × m 2H = g 2 4 500 (0.05)2 × =2m 10 0.5 So, At a horizontal distance of 2 m from the free end of the spring. Example 70 A rigid body of mass m is held at a height H on two smooth wedges of mass M each of which are themselves at rest on a horizontal frictionless floor. On releasing the body it moves down pushing aside the wedges. The velocity of recede of the wedges from each other when rigid body is at a height h from the ground is (A) 2mg(H − h) m + 2M (B) 2mg(H − h) 2m + M (C) 8mg(H − h) m + 2M Solution : Let speed of the wedge and the rigid body be V and respectively. Then applying wedge constraint we get V cos 45º = cos 45º V= ...(i) Using energy conservation, 1 1 mg(H – h) = 2 MV 2 + m2 2 2 From equation (i) and (ii) ...(ii) (D) 8mg(H − h) 2m + M WORK, POWER & ENERGY 2mg(H − h) m + 2M V= The velocity of recede of wedges from each other = 2 × V = So, answer is (C) Alter :Length of rod = x+y= 2 dx dy + =0 dt dt velocity of block = velocity of rod decrease in potential energy = increase in kinetic energy mg (H – h) = V= 2V = 1 1 1 mV2 + MV2 + MV2 2 2 2 2mg(H − h) 2M + m 8mg(H − h) 2M + m 8mg(H − h) m + 2M
Related Documents
- Chapter 5: Gravitation - Anwers
- Replication in Eukaryotes
- Bodies Concept - Study Notes
- Chapter 6: Mechanical Properties of Solids - Anwers
- Chapter 3: Motion in a Plane - Answers
- Chapter 11: Electric Current Through Conductors - Answers
- Chapter 10: Electrostatics - Answers
- Chapter 12: Magnetism - Answers
- Chapter 2: Mathematical Methods - Answers
- Chapter 4: Laws of Motion - Anwers
- Circles Questions and Answers
- Chapter 1: Units and Measurements - Answers
- Chapter 7: Thermal Properties of Matter - Anwers
- Chapter 8: Sound - Answers
- Chapter 9: Optics - Answers
- Achievements of Bohr's Theory
- Atomic Spectra of Hydrogen Atom
- Magnetic Circuit Questions and Answers
- Quantum Numbers - Lecture Note
- Coordinate System
Report
Tell us what’s wrong with it:
Thanks, got it!
We will moderate it soon!
Report
Tell us what’s wrong with it:
Free up your schedule!
Our EduBirdie Experts Are Here for You 24/7! Just fill out a form and let us know how we can assist you.
Take 5 seconds to unlock
Enter your email below and get instant access to your document